Leyes de Newton
jueves, 18 de mayo de 2017
miércoles, 17 de mayo de 2017
Rotación y traslacion
EQUILIBRIO TRASLACIONAL Y ROTACIONAL
Condiciones de equilibrio: Para que un cuerpo se encuentre en equilibrio, se requiere que la sumatoria de todas las fuerzas o torcas que actúan sobre él sea igual a cero. Se dice que todo cuerpo tiene dos tipos de equilibrio, el de traslación y el de rotación.
Traslación: Es aquel que surge en el momento en que todas las fuerzas que actúan sobre el cuerpo se nulifican, o sea, la sumatoria de las mismas sea igual a cero.
EFx = 0
EFy = 0
Rotación: Es aquel que surge en el momento en que todas las torcas que actúan sobre el cuerpo sean nulas, o sea, la sumatoria de las mismas sea igual a cero.
EMx= 0
EMy= 0
Aplicaciones: Se utiliza en todo tipo de instrumentos en los cuales se requiera aplicar una o varias fuerzas o torques para llevar a cabo el equilibrio de un cuerpo. Entre los instrumentos más comunes están la palanca,la balanza romana, la polea, el engrane, etc.
EJEMPLO DE PROBLEMA DE APLICACIÓN:
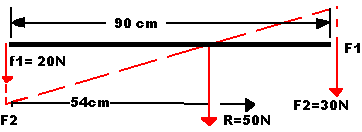
Una caja de 8 N está suspendida por un alambre de 2 m que forma un ángulo de 45° con la vertical. ¿Cuál es el valor de las fuerzas horizontal y en el alambre para que el cuerpo se mantenga estático?.
Primero se visualiza el problema de la siguiente manera:
A continuación se elabora su diagrama de cuerpo libre.
Ahora por medio de la descomposición de los vectores, calculamos la fuerza de cada uno de ellos.
F1x = - F1 cos 45°*
F1y = F1 sen 45°
F2x = F2 cos 0° = F2
F2y = F2sen0°=0
F3x = F3cos90°=0
F3y = - F3 sen 90° = - 8 N*
Porque los cuadrantes en los que se localizan son negativos.
Como únicamente conocemos los valores de F3, F2 y la sumatoria debe ser igual a cero en x e y, tenemos lo siguiente:
EFx=F1x+F2x+F3x=0
EFy=F1y+F2y+F3y=0
Por lo tanto tenemos lo siguiente:
EFx=-F1 cos 45+F2=0
F2=F1(0.7071)
EFy=-F1sen45-8N=0
8N=F1(0.7071)
F1=8N/0.7071=11.31 N
Para calcular F2, se sustituye F1 de la ecuación siguiente:
F2=F1(0.7071)
F2=11.31(0.7071)=8N
Traslación: Es aquel que surge en el momento en que todas las fuerzas que actúan sobre el cuerpo se nulifican, o sea, la sumatoria de las mismas sea igual a cero.
EFx = 0
EFy = 0
Rotación: Es aquel que surge en el momento en que todas las torcas que actúan sobre el cuerpo sean nulas, o sea, la sumatoria de las mismas sea igual a cero.
EMx= 0
EMy= 0
Aplicaciones: Se utiliza en todo tipo de instrumentos en los cuales se requiera aplicar una o varias fuerzas o torques para llevar a cabo el equilibrio de un cuerpo. Entre los instrumentos más comunes están la palanca,la balanza romana, la polea, el engrane, etc.
EJEMPLO DE PROBLEMA DE APLICACIÓN:
Una caja de 8 N está suspendida por un alambre de 2 m que forma un ángulo de 45° con la vertical. ¿Cuál es el valor de las fuerzas horizontal y en el alambre para que el cuerpo se mantenga estático?.
Primero se visualiza el problema de la siguiente manera:
A continuación se elabora su diagrama de cuerpo libre.
Ahora por medio de la descomposición de los vectores, calculamos la fuerza de cada uno de ellos.
F1x = - F1 cos 45°*
F1y = F1 sen 45°
F2x = F2 cos 0° = F2
F2y = F2sen0°=0
F3x = F3cos90°=0
F3y = - F3 sen 90° = - 8 N*
Porque los cuadrantes en los que se localizan son negativos.
Como únicamente conocemos los valores de F3, F2 y la sumatoria debe ser igual a cero en x e y, tenemos lo siguiente:
EFx=F1x+F2x+F3x=0
EFy=F1y+F2y+F3y=0
Por lo tanto tenemos lo siguiente:
EFx=-F1 cos 45+F2=0
F2=F1(0.7071)
EFy=-F1sen45-8N=0
8N=F1(0.7071)
F1=8N/0.7071=11.31 N
Para calcular F2, se sustituye F1 de la ecuación siguiente:
F2=F1(0.7071)
F2=11.31(0.7071)=8N
Leyes de Equilibrio
Las condiciones de equilibrio son las leyes que rigen la estática. La estática es la ciencia que estudia las fuerzas que se aplican a un cuerpo para describir un sistema en equilibrio. Diremos que un sistema está en equilibrio cuando los cuerpos que lo forman están en reposo, es decir, sin movimiento. Las fuerzas que se aplican sobre un cuerpo pueden ser de tres formas:
-Fuerzas angulares: Dos fuerzas se dice que son angulares, cuando actúan sobre un mismo punto formando un ángulo.
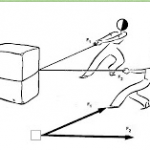
-Fuerzas colineales: Dos fuerzas son colineales cuando la recta de acción es la misma, aunque las fuerzas pueden estar en la misma dirección o en direcciones opuestas.
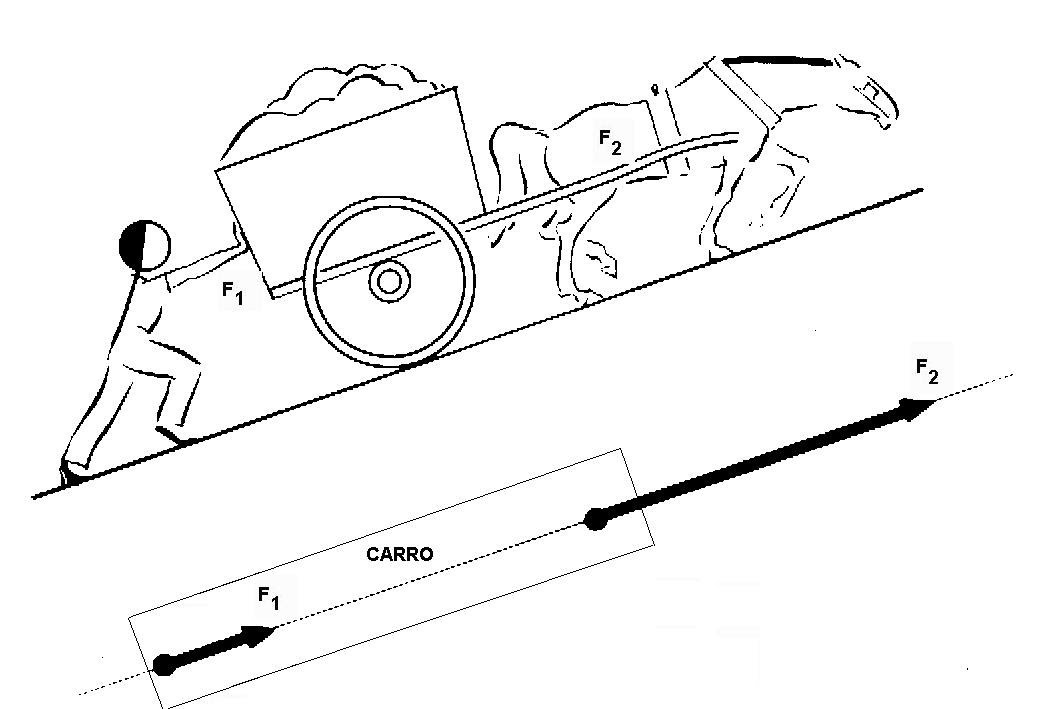
-Fuerzas paralelas: Dos fuerzas son paralelas cuando sus direcciones son paralelas, es decir, las rectas de acción son paralelas, pudiendo también aplicarse en la misma dirección o en sentido contrario.
A nuestro alrededor podemos encontrar numerosos cuerpos que se encuentran en equilibrio. La explicación física para que esto ocurra se debe a las condiciones de equilibrio:
-Fuerzas angulares: Dos fuerzas se dice que son angulares, cuando actúan sobre un mismo punto formando un ángulo.

-Fuerzas colineales: Dos fuerzas son colineales cuando la recta de acción es la misma, aunque las fuerzas pueden estar en la misma dirección o en direcciones opuestas.

-Fuerzas paralelas: Dos fuerzas son paralelas cuando sus direcciones son paralelas, es decir, las rectas de acción son paralelas, pudiendo también aplicarse en la misma dirección o en sentido contrario.

A nuestro alrededor podemos encontrar numerosos cuerpos que se encuentran en equilibrio. La explicación física para que esto ocurra se debe a las condiciones de equilibrio:
-Primera condición de equilibrio: Diremos que un cuerpo se encuentra en equilibrio de traslación cuando la fuerza resultante de todas las fuerzas que actúan sobre él es nula: ∑ F = 0.
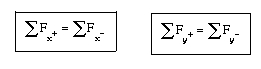
Desde el punto de vista matemático, en el caso de fuerzas coplanarias, se tiene que cumplir que la suma aritmética de las fuerzas o de sus componentes que están el la dirección positiva del eje X sea igual a las componentes de las que están en la dirección negativa. De forma análoga, la suma aritmética de las componentes que están en la dirección positiva del eje Y tiene que ser igual a las componentes que se encuentran en la dirección negativa:
Por otro lado, desde el punto de vista geométrico, se tiene que cumplir que las fuerzas que actúan sobre un cuerpo en equilibrio tienen un gráfico con forma de polígono cerrado; ya que en el gráfico de las fuerzas, el origen de cada fuerza se representa a partir del extremo de la fuerza anterior, tal y como podemos observar en la siguiente imagen.
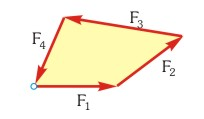
El hecho de que su gráfico corresponda a un polígono cerrado verifica que la fuerza resultante sea nula, ya que el origen de la primera fuerza (F1) coincide con el extremo de la última (F4).
Desde el punto de vista matemático, en el caso de fuerzas coplanarias, se tiene que cumplir que la suma aritmética de las fuerzas o de sus componentes que están el la dirección positiva del eje X sea igual a las componentes de las que están en la dirección negativa. De forma análoga, la suma aritmética de las componentes que están en la dirección positiva del eje Y tiene que ser igual a las componentes que se encuentran en la dirección negativa:

Por otro lado, desde el punto de vista geométrico, se tiene que cumplir que las fuerzas que actúan sobre un cuerpo en equilibrio tienen un gráfico con forma de polígono cerrado; ya que en el gráfico de las fuerzas, el origen de cada fuerza se representa a partir del extremo de la fuerza anterior, tal y como podemos observar en la siguiente imagen.

El hecho de que su gráfico corresponda a un polígono cerrado verifica que la fuerza resultante sea nula, ya que el origen de la primera fuerza (F1) coincide con el extremo de la última (F4).
-Segunda condición de equilibrio: Por otro lado, diremos que un cuerpo está en equilibrio de rotación cuando la suma de todas las fuerzas que se ejercen en él respecto a cualquier punto es nula. O dicho de otro modo, cuando la suma de los momentos de torsión es cero.
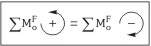
En este caso, desde el punto de vista matemático, y en el caso anterior en el que las fuerzas son coplanarias; se tiene que cumplir que la suma de los momentos o fuerzas asociados a las rotaciones antihorarias (en el sentido contrario de las agujas del reloj), tiene que ser igual a la suma aritmética de los momentos o fuerzas que están asociados a las rotaciones horarias (en el sentido de las agujas del reloj):
En este caso, desde el punto de vista matemático, y en el caso anterior en el que las fuerzas son coplanarias; se tiene que cumplir que la suma de los momentos o fuerzas asociados a las rotaciones antihorarias (en el sentido contrario de las agujas del reloj), tiene que ser igual a la suma aritmética de los momentos o fuerzas que están asociados a las rotaciones horarias (en el sentido de las agujas del reloj):
Un cuerpo se encuentra en equilibrio traslacional y rotacional cuando se verifiquen de forma simultánea las dos condiciones de equilibrio. Estas condiciones de equilibrio se convierten, gracias al álgebra vectorial, en un sistema de ecuaciones cuya solución será la solución de la condición del equilibrio.
Equilibrio
Equilibrio
El estudio del equilibrio de los cuerpos bajo la acción de un sistema de fuerzas es el objeto de la estática, que es una parte de la física de decisiva importancia en aspectos tales como la determinación de la estabilidad de una construcción metálica, el diseño de un puente colgante o el cálculo de cualquier estructura de una obra civil.El manejo de los sistemas de fuerzas, incluyendo las del peso y las de reacción, y el cálculo de la magnitud momento constituyen elementos esenciales de esta ciencia del equilibrio mecánico.
Las características que definen un cuerpo material están directa o indirectamente relacionadas con las fuerzas. Todos los cuerpos pueden ser considerados como agregados de partículas unidas entre sí por fuerzas cuya intensidad varía desde la débil atracción gravitatoria, en el caso de una nebulosa, hasta las intensas fuerzas eléctricas de enlace entre los átomos de carbono en un cristal de diamante.
En ambos casos extremos es un conjunto de fuerzas el que hace que las diferentes partículas componentes constituyan un todo. Cuando un sistema de fuerzas es tal que cancelan mutuamente sus efectos, se tiene una situación de equilibrio.
El sistema de fuerzas entre los átomos del carbono en el diamante es tal, que sus efectos se cancelan mutuamente y el sólido permanece en equilibrio sin ninguna fuerza exterior que actúe sobre él.
El equilibrio de los cuerpos se caracteriza por la ausencia de cambios en su movimiento. El reposo es un tipo particular de equilibrio cuya importancia se hace manifiesta, como condición de estabilidad, en un edificio, en un puente o en una torre. Sin embargo, el equilibrio de un sólido no se reduce solamente a la ausencia de movimiento.
Un cuerpo se puede estar moviendo en línea recta con velocidad constante o girando uniformemente alrededor de un eje y, sin embargo, hallarse en equilibrio. Es entonces la ausencia de aceleración y no la ausencia de velocidad lo que define en física la noción de equilibrio.
Del estudio de las condiciones generales de equilibrio de los cuerpos y de su aplicación en situaciones diversas se ocupa la estática, que puede ser considerada, por tanto como la ciencia del equilibrio.
Clases de Equilibrio:
Equilibrio Completo
Un cuerpo rígido está en equilibrio completo cuando se encuentra en equilibrio de traslación.
Equilibrio de Rotación
Un Cuerpo esta en equilibrio de rotación cuando la suma algebraica de los momentos de paz fuerzas que actúan sobre el es igual a cero.
Equilibrio de Traslación
Un Cuerpo esta en equilibrio de traslación cuando la suma algebraica de las fuerzas aplicadas sobre el es igual a cero.
Equilibrio Estable
Un Cuerpo suspendido esta en equilibrio estable cuando el centro de suspencsion esta por encima del centro de gravedad.
Equilibrio Indiferente
Un Cuerpo suspendido esta en el equilibrio indiferente cuando el centro de su suspensión coincide con el centro de gravedad.
Equilibrio Inestable
Un Cuerpo suspendido esta en equilibrio inestable cuando el centro de su suspension esta por debajo del centro de gravedad.
Estática
Estática
La estática es la rama de la mecánica clásica que analiza las cargas (fuerza, par / momento) y estudia el equilibrio de fuerzas en los sistemas físicos en equilibrio estático, es decir, en un estado en el que las posiciones relativas de los subsistemas no varían con el tiempo. La primera ley de Newton implica que la red de la fuerza y el par neto (también conocido como momento de fuerza) de cada organismo en el sistema es igual a cero. De esta limitación pueden derivarse cantidades como la carga o la presión. La red de fuerzas de igual a cero se conoce como la primera condición de equilibrio, y el par neto igual a cero se conoce como la segunda condición de equilibrio.
La estática proporciona, mediante el empleo de la mecánica del sólido rígido, solución a los problemas denominados isostáticos. En estos problemas, es suficiente plantear las condiciones básicas de equilibrio, que son:
- El resultado de la suma de fuerzas es nulo.
- El resultado de la suma de momentos respecto a un punto es nulo.
- Estas dos condiciones, mediante el álgebra vectorial, se convierten en un sistema de ecuaciones; la resolución de este sistema de ecuaciones es la solución de la condición de equilibrio.
- Existen métodos de resolución de este tipo de problemas estáticos mediante gráficos, heredados de los tiempos en que la complejidad de la resolución de sistemas de ecuaciones se evitaba mediante la geometría, si bien actualmente se tiende al cálculo por ordenador.
Para la resolución de problemas hiperestáticos (aquellos en los que el equilibrio se puede alcanzar con distintas combinaciones de esfuerzos) es necesario considerar ecuaciones de compatibilidad. Dichas ecuaciones adicionales de compatibilidad se obtienen mediante la introducción de deformaciones y tensiones internas asociadas a las deformaciones mediante los métodos de la mecánica de sólidos deformables, que es una ampliación de la mecánica del sólido rígido que, además, da cuenta de la deformabilidad de los sólidos y sus efectos internos.
Existen varios métodos clásicos basados en la mecánica de sólidos deformables, como los teoremas de Castigliano o las fórmulas de Navier-Bresse.
Suma de fuerzas: Cuando sobre un cuerpo o sólido rígido actúan varias fuerzas que se aplican en el mismo punto, el cálculo de la fuerza resultante resulta trivial: basta sumarlas vectorialmente y aplicar el vector resultante en el punto común de aplicación.
Sin embargo, cuando existen fuerzas con puntos de aplicación diferentes es necesario determinar el punto de aplicación de la fuerza resultante. Para fuerzas no paralelas esto puede hacerse sumando las fuerzas dos a dos. Para ello se consideran dos de las fuerzas trazan rectas prolongando las fuerzas en ambos sentidos y buscando su intersección. Esa intersección será un punto de paso de la fuerza suma de las dos. A continuación se substituyen las dos fuerzas por una única fuerza vectorial suma de las dos anteriores aplicada en el punto de intersección. Esto se repite n-1 veces para un sistema de n fuerzas y se obtiene el punto de paso de la resultante.
Este algoritmo puede ser bastante pesado para un número de fuerzas elevado. Además cuando varias de las fuerzas son paralelas puede no funcionar. Para hacer más rápido el cálculo del punto de paso puede usarse en el caso de fuerzas coplanares el método del polígono funicular, que es computacionalmente más rápido y aplicable también al caso de que todas las fuerzas sean paralelas (y por tanto sus rectas de acción, sin puntos de intersección).
La estática proporciona, mediante el empleo de la mecánica del sólido rígido, solución a los problemas denominados isostáticos. En estos problemas, es suficiente plantear las condiciones básicas de equilibrio, que son:
- El resultado de la suma de fuerzas es nulo.
- El resultado de la suma de momentos respecto a un punto es nulo.
- Estas dos condiciones, mediante el álgebra vectorial, se convierten en un sistema de ecuaciones; la resolución de este sistema de ecuaciones es la solución de la condición de equilibrio.
- Existen métodos de resolución de este tipo de problemas estáticos mediante gráficos, heredados de los tiempos en que la complejidad de la resolución de sistemas de ecuaciones se evitaba mediante la geometría, si bien actualmente se tiende al cálculo por ordenador.
Para la resolución de problemas hiperestáticos (aquellos en los que el equilibrio se puede alcanzar con distintas combinaciones de esfuerzos) es necesario considerar ecuaciones de compatibilidad. Dichas ecuaciones adicionales de compatibilidad se obtienen mediante la introducción de deformaciones y tensiones internas asociadas a las deformaciones mediante los métodos de la mecánica de sólidos deformables, que es una ampliación de la mecánica del sólido rígido que, además, da cuenta de la deformabilidad de los sólidos y sus efectos internos.
Existen varios métodos clásicos basados en la mecánica de sólidos deformables, como los teoremas de Castigliano o las fórmulas de Navier-Bresse.
Suma de fuerzas: Cuando sobre un cuerpo o sólido rígido actúan varias fuerzas que se aplican en el mismo punto, el cálculo de la fuerza resultante resulta trivial: basta sumarlas vectorialmente y aplicar el vector resultante en el punto común de aplicación.
Sin embargo, cuando existen fuerzas con puntos de aplicación diferentes es necesario determinar el punto de aplicación de la fuerza resultante. Para fuerzas no paralelas esto puede hacerse sumando las fuerzas dos a dos. Para ello se consideran dos de las fuerzas trazan rectas prolongando las fuerzas en ambos sentidos y buscando su intersección. Esa intersección será un punto de paso de la fuerza suma de las dos. A continuación se substituyen las dos fuerzas por una única fuerza vectorial suma de las dos anteriores aplicada en el punto de intersección. Esto se repite n-1 veces para un sistema de n fuerzas y se obtiene el punto de paso de la resultante.
Este algoritmo puede ser bastante pesado para un número de fuerzas elevado. Además cuando varias de las fuerzas son paralelas puede no funcionar. Para hacer más rápido el cálculo del punto de paso puede usarse en el caso de fuerzas coplanares el método del polígono funicular, que es computacionalmente más rápido y aplicable también al caso de que todas las fuerzas sean paralelas (y por tanto sus rectas de acción, sin puntos de intersección).
Historia de la Fisica
La Historia de la Fisica
La opinión generalizada es que la ciencia y la era científica comenzaron en el siglo XVII con Isaac Newton dando forma a las matemáticas que pretendían describir nuestro mundo físico.
Durante más de doscientos años, las observaciones que hizo Newton sobre la naturaleza fueron la base de la rama científica conocida como “física clásica”, teniendo mucho éxito al explicar las cosas a gran escala como el movimiento de los planetas y el hecho de que las manzanas caigan de un árbol (antes eureka, hoy: wow!). La física clásica ha hecho tan bien su trabajo que nos ha permitido calcurar las órbitas de nuestros satélites e incluso pese a todo enviar cohetes a la luna ida y vuelta.
En los inicios del siglo XX, sin embargo, los avances científicos revelaron un lugar de la naturaleza en el que las leyes de Newton no parecían funcionar : en el mundo microscópico del átomo, entonces fué necesario desarrollar un nuevo tipo de física: la física cuántica.
Cuántica viene de Quantum que quiere decir una determinada cantidad de energía electromagnética. Por lo tanto el quantum es la sustanciade la que está hecho nuestro mundo cuando lo reducimos a su quintaesencia. Los científicos de la física cuántica pronto comprobaron que lo que a nosotros nos parece un mundo sólido, en realidad no lo es en absoluto. Un buen ejemplo es que al igual que la unión de muchas imágenes individuales hace que una película parezca real, la vida está compuesta de pequeños y breves “paquetes” de luz llamados “quanta”. Los quanta de la vida suceden tan rápidamente que a menos que nuestro cerebro haya sido adiestrado para funcionar de otra manera (desarrollando el testigo, el observador, ralentizando los movimientos a través de técnicas de meditación por ejemplo) simplemente suma todos los impulsos para crear la acción ininterrumpida semejante a cualquier película proyectada sobre una pantalla blanca.
La física cuántica es el estudio de lo que sucede a muy pequeña escala con las fuerzas que dan vida a nuestro mundo físico.
Ahora bien, hay una tercera forma de física y es la que quiere unir a estas dos físicas: clásica y cuántica, sería la llamada teoría unificada. Hacer esto requiere la existencia de algo que llene aquello que consideramos como espacio vacío. Y a eso mismo es donde queremos llegar: es lo que sería el origen de la Matrix.
Resumiendo hasta llegar a la teoría Unificada:
1687 – Física newtoniana: Isaac Newton publica sus leyes del movimiento, y así comienza la ciencia moderna. Según esta visión, el universo es un enorme sistema mecánico en que el tiempo y el espacio son absolutos.
1867 – Física de la teoría de campo: James Clerk Maxwell propone la existencia de fuerzas que no pueden ser explicadas por la física de Newton. Sus investigaciones, junto con las de Michael Faraday, llevan a la visión de un universo compuesto por campos de energía que interactúan mutuamente.
1900 – Física cuántica: Max Planck publica su teoría de un mundo compuesto de «paquetes» de energía llamados «quanta». Los experimentos realizados a escala cuántica muestran que la materia existe más como probabilidades y tendencias que como algo absoluto, lo que indica que la «realidad» puede no ser tan real y sólida como creíamos.
1905 – Física de la relatividad: la visión del universo de Albert Einstein desbanca a la física newtoniana. Einstein sugiere que el tiempo es relativo en lugar de absoluto. Un aspecto clave de la relatividad es que el tiempo y el espacio no pueden ser separados y existen juntos como una cuarta dimensión.
1970 – Física de la teoría de cuerdas: los físicos descubren que se pueden usar las teorías que describen el universo como compuesto por pequeñas cuerdas vibratorias de energía para explicar tanto el mundo cuántico como el de la realidad cotidiana. En 1984, la teoría es formalmente aceptada por la comunidad científica como un puente que puede servir para unir todas las teorías.
20?? – La nueva y mejorada teoría unificada de la física: algún día en el futuro, los físicos descubrirán una forma para explicar la naturaleza holográfica de lo que observamos en el universo cuántico, así como lo que vemos en el mundo de la realidad cotidiana. Formularán las ecuaciones que unifiquen sus explicaciones y formen una única historia.
Siglo XVIII: termodinámica y óptica
A partir del siglo XVIII Boyle y Young desarrollaron la termodinámica. En 1733 Bernoulli usó argumentos estadísticos, junto con la mecánica clásica, para extraer resultados de la termodinámica, iniciando la mecánica estadística. En 1798 Thompson demostró la conversión del trabajo mecánico en calor y en 1847 Joule formuló la ley de conservación de la energía.En el campo de la óptica el siglo XVIII comenzó con la teoría corpuscular de la luz de Newton expuesta en su famosa obra Opticks. Aunque las leyes básicas de la óptica geométrica habían sido descubiertas algunas décadas antes, el siglo XVIII fue bueno en avances técnicos en este campo produciéndose las primeras lentes acromáticas, midiéndose por primera vez la velocidad de la luz y descubriendo la naturaleza espectral de la luz. El siglo concluyó con el célebre experimento de Young de 1801 en el que se ponía de manifiesto la interferencia de la luz demostrando la naturaleza ondulatoria de ésta.
Siglo XIX: electromagnetismo y estructura atómica
La investigación física de la primera mitad del siglo XIX estuvo dominada por el estudio de los fenómenos de la electricidad y el magnetismo. Coulomb, Luigi Galvani, Faraday, Ohm y muchos otros físicos famosos estudiaron los fenómenos dispares y contraintuitivos que se asocian a este campo. En 1855 Maxwell unificó las leyes conocidas sobre el comportamiento de la electricidad y el magnetismo en una sola teoría con un marco matemático común mostrando la naturaleza unida del electromagnetismo. Los trabajos de Maxwell en el electromagnetismo se consideran frecuentemente equiparables a los descubrimientos de Newton sobre la gravitación universal y se resumen con las conocidas, ecuaciones de Maxwell, un conjunto de cuatro ecuaciones capaz de predecir y explicar todos los fenómenos electromagnéticos clásicos. Una de las predicciones de esta teoría era que la luz es una onda electromagnética. Este descubrimiento de Maxwell proporcionaría la posibilidad del desarrollo de la radio unas décadas más tarde por Heinrich Hertz en 1888.En 1895 Roentgen descubrió los rayos X, ondas electromagnéticas de frecuencias muy altas. Casi simultáneamente, Henri Becquerel descubría la radioactividad en 1896. Este campo se desarrolló rápidamente con los trabajos posteriores de Pierre Curie, Marie Curie y muchos otros, dando comienzo a la física nuclear y al comienzo de la estructura microscópica de la materia.en 1897 Thomson descubrió el electrón, la partícula elemental que transporta la corriente en los circuitos eléctricos proponiendo en 1904 un primer modelo simplificado del átomo.
Siglo XX: segunda revolución de la física
El siglo XX estuvo marcado por el desarrollo de la física como ciencia capaz de promover el desarrollo tecnológico. A principios de este siglo los físicos consideraban tener una visión casi completa de la naturaleza. Sin embargo pronto se produjeron dos revoluciones conceptuales de gran calado: El desarrollo de la teoría de la relatividad y el comienzo de la mecánica cuántica.En 1905 Albert Einstein, formuló la teoría de la relatividad especial, en la cual el espacio y el tiempo se unifican en una sola entidad, el espacio-tiempo. La relatividad formula ecuaciones diferentes para la transformación de movimientos cuando se observan desde distintos sistemas de referencia inerciales a aquellas dadas por la mecánica clásica. Ambas teorías coinciden a velocidades pequeñas en relación a la velocidad de la luz. En 1915 extendió la teoría especial de la relatividad para explicar la gravedad, formulando la teoría general de la relatividad, la cual sustituye a la ley de la gravitación de Newton.En 1911 Rutherford dedujo la existencia de un núcleo atómico cargado positivamente a partir de experiencias de dispersión de partículas. A los componentes de carga positiva de este núcleo se les llamó protones. Los neutrones, que también forman parte del núcleo pero no poseen carga eléctrica, los descubrió Chadwick en 1932.
Física del siglo XXI
La física sigue enfrentándose a grandes retos, tanto de carácter práctico como teórico, a comienzos del siglo XXI. El estudio de los sistemas complejos dominados por sistemas de ecuaciones no lineales, tal y como la meteorología o las propiedades cuánticas de los materiales que han posibilitado el desarrollo de nuevos materiales con propiedades sorprendentes. A nivel teórico la astrofísica ofrece una visión del mundo con numerosas preguntas abiertas en todos sus frentes, desde la cosmología hasta la formación planetaria. La física teórica continúa sus intentos de encontrar una teoría física capaz de unificar todas las fuerzas en un único formulismo en lo que sería una teoría del todo. Entre las teorías candidatas debemos citar a la teoría de supercuerdas.El descubrimiento de la expansión acelerada del universo llevó a un interés renovado por la cosmología, en particular a los trabajos teóricos sobre la energía oscura y la materia oscura. Además el trabajo de Juan Martín Maldacena sobre la "correspondencia AdS/CFT" arrojaría nueva luz sobre otra conjetura física conocida como principio holográfico.El período que va de 1973 a 2017 ha sido considerado por algunos físicos importantes como Lee Smolin y otros, un período excepcional ya que durante él se hicieron proporcionalmente menos teóricos nuevos que durante otros períodos del siglo XX, estando la física dominada por teorías altamente especulativas sobre las que ha sido difícil obtener evidencias empíricas que permitan un avance seguro. Gran parte de los éxitos experimentales como la detección de los bosones W y Z, o la detección del bosón de Higgs son confirmaciones de teorías desarrolladas con anterioridad a 1975, por lo que realmente no son confirmaciones de las teorías en las que han trabajado los físicos teóricos en las últimas décadas
Suscribirse a:
Comentarios (Atom)











